annexe 0b
Wikipédia et les informations fausses
Article Projection de Mercator, et Cours des Glénans
IMPORTANTE INFORMATION PRÉALABLE À L’ATTENTION DU LECTEUR
DEPUIS LA PARUTION DE CE SITE (MAI 2020) L’ARTICLE DE WIKIPÉDIA A ÉTÉ TOTALEMENT MODIFIÉ. IL EST DORÉNAVANT EXACT !
LE TEXTE QUI SUIT SE RAPPORTE À LA VERSION FAUSSE, celle qui existait dans WIKIPEDIA QUAND IL A ÉTÉ ÉCRIT.
ON PEUT AISEMENT La RETROUVER EN UTILISANT L’HISTORIQUE.
En revanche et bien évidemment ce qui est écrit dans le Cours des Glénans est toujours faux.
Les principes
On sait la profession de foi de Wikipédia : un projet collaboratif et communautaire, adressé à tout le monde, soumis au seul consensus pour permettre d’élaborer une encyclopédie d’une qualité dont on attend qu’elle soit meilleure que celle d’une encyclopédie uniquement écrite par des « sachants ».
Voilà qui a fait son succès en présentant tant d’excellents articles fondés sur plusieurs principes dont on en retient ici deux :
◊ Principe 1 : il n’y a pas de Comité de lecture et donc d’évaluation par les pairs pour garantir la qualité d’un article. Chacun – tout le monde – peut intervenir quand il le veut sur l’ensemble des articles de l’encyclopédie.
◊ Principe 2 : au motif éminemment recevable d’interdire que Wikipédia devienne une tribune, cette encyclopédie bannit toute synthèse. Seules comptent les sources1.
Les sources, seulement les sources
Or de nombreux domaines ne sont connus que par des sources qui ne s’accordent pas toujours bien entre elles, voire s’opposent.
D’où de nombreux cas où l’examen des sources et donc leur synthèse s’imposerait. Or elle sera refusée car considérée2 comme un « Travail Inédit », inédit et donc interdit dans cette encyclopédie qui impose d’écrire exclusivement à partir de sources.
Il est donc simple d’y éditer des articles totalement faux. Il suffit de s’appuyer sur de sources fausses.
Donnons un exemple parce qu’il est emblématique et facile d’accès3.
Les lecteurs passionnés de la mer – il y en a beaucoup qui y naviguent chaque année et c’est pour cela que l’on choisit cet exemple – les passionnés de mer donc utilisent des cartes marines4 établies selon la projection de Mercator.
Chers lecteurs, gardez-vous bien de consulter Wikipédia pour vous informer de ce qu’est une projection de Mercator.
Ce qui y est dit dans l’article « Projection de Mercator » y est entièrement faux dès les premières lignes qui parlent de conservation des angles.
Toutes les sources utilisées méconnaissent la réalité de la projection de Mercator. Pire, on va montrer plus bas qu’une source qui d’évidence aurait dû être utilisée, le Nouveau Cours des Glénans, est fausse elle aussi.
Si ce qui y est dit dans l’article de Wikipédia était vrai
◊ si, partant d’un angle se trouvant naturellement sur la Terre entre deux côtés courbes et donc sphériques (la Terre étant considérée comme une sphère ce qu’elle n’est pas d’ailleurs) ;
◊ si, comme il est indiqué, on projette (par une lumière placée au centre de la Terre) les deux côtés de cet angle sur un cylindre tangent à l’équateur – ce qui a pour conséquence qu’on ne sait plus ce que deviennent ces côtés qui peuvent être droits ou courbes (et quelle courbe ?) selon l’angle de projection ;
◊ si, alors, on déplie le cylindre ce qui aplatit les deux côtés, maintenant courbés selon le cylindre, d’un angle dont ne sait déjà plus quel il est ;
◊ et si enfin l’angle de départ sur la sphère se trouve égal à l’angle final sur la carte plate comme il est dit…
… alors on serait en présence d’un miracle mathématique à enseigner illico à l’École Polytechnique et dans toutes les écoles d’ingénieurs de France et de Navarre en même temps que les miracles de Lourdes.
Quant à Mercator, s’il avait agi ainsi, il aurait reçu la médaille Fields à titre posthume.
Qu’en est-il ?
Le principe mis en avant par Wikipédia a ses limites. Celles où la communauté qui publie ignore de quoi elle parle en s’appuyant sur de sources dont elle ne peut mesurer la qualité.
Au lecteur intéressé on propose de se reporter à un vrai traité de navigation que les nombreux intervenants qui ont écrit cet article de Wikipédia n’ont pas consulté.
À savoir5 le Traité Vagnon de Navigation notamment utilisé à l’École Navale qui forme les officiers de la Marine Nationale, même s’il présente une petite erreur de coefficient qui a été signalée à l’auteur. Une erreur mineure que l’ancien professeur de navigation que nous sommes peut observer et qui ne change rien à la bonne compréhension de la projection.
Attention ! Une projection au sens mathématique du terme qui n’a évidemment rien à voir, absolument rien à voir, avec la projection cinématographique des frères Lumière et l’illumination moderne à partir de faisceaux lasers placés au centre de la Terre.
Le COMBLE
Cet article sur la carte de Mercator nous montre comment l’incompétence partagée d’intervenants assez nombreux et d’accord entre eux sans mesurer leur ignorance commune permet, en citant nombre de sources fausses, la parution d’un article tout aussi faux.
Mais le comble, y compris pour Wikipédia, c’est la source « Le Cours des Glénans ».
Les intervenants qui ont écrit l’article auraient dû citer et prendre en compte le récent traité de navigation des Glénans6.
Quand on parle, et cela depuis la fin de la dernière guerre et la montée en puissance de la navigation de plaisance aux Glénans, de ce qui touche à la navigation en général et ici de la projection de Mercator en particulier, ne pas s’intéresser au Nouveau cours de navigation des Glénans – précédemment appelé ainsi et qui en est à sa huitième édition (2017) sous le titre Le Cours des Glénans – est regrettable pour ne pas dire inadmissible.
Ne pas en avoir parlé, c’est signe pour qui ceux ont écrit dans l’article Projection de Mercator dans Wikipédia qu’ils auraient gagné à s’abstenir de publier sur un sujet auquel ils ne connaissent pas, d’évidence, où sont les bonnes sources. La renommée des Glénans n’est plus à faire.
Mais il se trouve, chose étonnante, que dans la huitième édition du Cours des Glénans qui aurait dû être prise en compte, la présentation qui y est faite de la carte de Mercator est fausse.
Fausse répétons-le. Alors qu’elle était exacte -par exemple – dans l’édition7 de du Cours des Glénans de 1974.
Satisfaire l’objectif de Wikipédia de présenter la connaissance à partir des sources les plus récentes comme le demande l’encyclopédie peut se révéler très dangereux.
Cela dit, on est évidemment en droit de se demander pourquoi l’excellent Cours des Glénans est devenu récemment faux.
Une hypothèse s’impose. Le rédacteur, à l’époque où le Cours était exact, n’est plus. Il a été remplacé par un ignorant. Pire, cet ignorant pourrait s’informer dans Wikipédia.
Ainsi et malheureusement – il est très difficile de l’éviter8 – l’encyclopédie Wikipédia propage-t-elle (parfois et très rarement) le faux dans des articles dont le texte sonne le vrai.
Conclusion
WIKIPEDIA : la remarque qui s’impose
Wikipédia, on l’a dit, affiche une position de principe: ceux qui ne savent pas sont capables d’élaborer une encyclopédie d’un intérêt supérieur à celle qui serait éditée par ceux qui savent.
Il est seulement demandé de s’appuyer sur des sources publiées. Et d’utiliser un pseudonyme. Les sachants ne doivent pas s’imposer par leur nom.
La remarque est que tout cela a des limites. L’article qui induisait le lecteur en erreur sur le carte de Mercator est là pour le démontrer.
Il a d’évidence été écrit par des non-sachants qui, sans expérience du dossier, se sont appuyés sur des articles issus notamment de la marine Marchande qui étaient faux. Auraient-ils lu le dernier Cours des Glénans, faux aussi, qu’il en aurait été de même.
Ils n’ont pris aucunement en compte les publications qui auraient pu montrer qu’il était urgent de réfléchir avant d’écrire et dire le faux aux lecteurs. D’ailleurs, l’auraient-ils fait qu’il n’auraient pas été capables de démêler le vrai du faux.
Or les publications qui disent vrai sur la carte de Mercator sont nombreuses.
Nous avons cité le Traité Vagnon de Navigation.
Nous voulons signaler ici à l’attention du lecteur le Math-Jeunes n°115, 2006 de la Société Belge des Professeurs de Mathématique d’expression française, particulièrement intéressant par son aspect historique.
Nous remercions Monsieur Hugues Masy qui y publie un « Mercator, les marins et les mathématiciens » pour la correspondance qu’il a bien voulu avoir avec le rédacteur de ce site.
Nous retenons de lui que parler de projection sur un cylindre c’est, selon, ses propres termes, « faire injure à Mercator en minimisant radicalement l’intelligence créatrice qu’il a effectivement développée en concevant sa carte nautique et qui a irrigué la naissance de l’analyse mathématique ».
N’hésitons pas à le répéter: le cylindre n’a rien à voir, n’a aucune place dans la projection – au sens mathématique – de Mercator !
POUR LE LECTEUR QUI VEUT ALLER PLUS LOIN
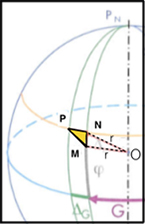
Construction de la carte
Construire la carte c’est projeter sur son plan le triangle élémentaire PNM de la sphère (à gauche) auquel doit être semblable le triangle élémentaire pnm sur la carte (à droite).
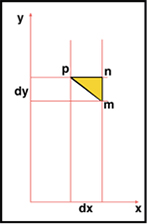
Pour le plan
On définit les côtés du triangle élémentaire pnp :
pn = dx
nm = dy
On définit ensuite le coefficient U qui donnera la longueur sur le plan représenté une minute de longitude. Les calculs qui suivent sont relatifs au Planisphère terrestre n° 0101H du Service Hydrographique de la Marine où 99,8 cm couvrent les 360° du 120°Est au 120°Ouest. On a :
99,8 cm = U x 360° x 60’ soit U = 99,8/360x 60= 0,004620
Une minute de longitude est représentée par :
1 U = 1x 0,00462 = 0,00462 cm
Plus généralement :
x = U G (longitude) et dx = U dG
D’où la nouvelle définition des deux côtés du triangle sous la forme :
pn = U dG (dG en minutes d’arc)
nm = dy
Pour la sphère
On définit le côtés du triangle élémentaire PNP :
PN = r cosØ dG
NM = r dØ
où :
r = rayon de la Terre
Ø latitude et G longitude s’expriment en degrés radian.
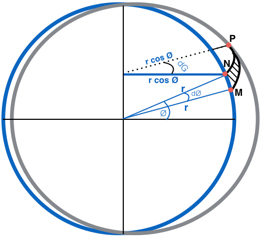
On doit alors tout exprimer dans un même unité. On choisit le degré radian avec :
π radian = 180° x 60’ = 10.800 minutes d’arc
Soit :
1 radian = 180 x 60 / π = 3437, 74 minutes d’arc
Les côtés du triangle élémentaire de la carte deviennent :
pn = 3437,74 U dG
mn = dy
et ceux de la sphère sont :
PN = r cosØ dG
NM = r dØ
On peut en venir alors à l’expression de la projection qui veut que le deux triangles PNP et pnp soient semblables, ce qui s’écrit (on a arrondi 3437,74 ainsi qu’on le voit dans les ouvrages de navigation qui traitent de la carte de Mercator) :
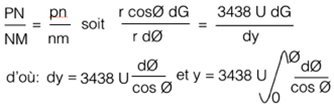
On trouve aujourd’hui très facilement le résultat de l’intégrale de dØ/cosØ (voir Internet : Fonction de Gudermann).
Il vient :
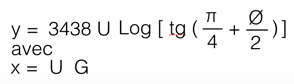
Pour le parallèle 45° de la carte 0101H, on obtient :
y= 3437,74 x 0,0046 x Log [ tg (45°+ 22,5°) ] = 3437,74 x 0,0046 x Log [2,41]
y = 3437,74 x 0,0046 x 0,88 = 13,9 cm
C’est la valeur que l’on lit sur le planisphère de Mercator 0101H, à très peu près. La Terre n’est pas sphérique.
notes
- 1 | Voir : https://fr.wikipedia.org/wiki/Aide:Présentez_vos_sources
https://fr.wikipedia.org/wiki/Wikipédia:Citez_vos_sources
https://fr.wikipedia.org/wiki/Wikipédia:Vérifiabilité - 2 | Voir : https://fr.wikipedia.org/wiki/Wikipédia:Travaux_inédits
- 3 | Voir : https://fr.wikipedia.org/wiki/Projection_de_Mercator (À la date de parution de notre site).
- 4 | Presque toutes. Peu de lecteurs naviguent dans l’océan glacial arctique, près du pôle Nord. Les cartes utilisées n’utilisent pas la projection de Mercator.
- 5 | Traité Vagnon de Navigation, Vagnon-Fleurus Éditions 2015.
- 6 | Le Cours des Glénans, Huitième édition, Éditions du Seuil, 2017.
- 7 | Nouveau Cours de navigation des Glénans, Éditions du Seuil - Éditions du Compas, 1972.
- 8 | Notre expérience décrite dans ce site nous conduit à penser que celui qui, tout seul, dirait dans la page de discussion d’un article qu’il est faux se trouverait devant des pseudonymes agissant à la façon des pseudonymes Heurtelions, Correcteur21, Iyy ou encore Keranplein et autres qui se ligueraient contre lui pour interdire toute modification.
